Maxwell-Boltzmann Distribution

Next: Collision Parameters Up: Gases and Ideal Gases Previous: Kinetic Gas Theory Contents Index

Maxwell-Boltzmann Distribution

The kinetic energy distribution of electrons, ions and neutrals is very important for characterizing a gas. From statistical arguments and also from experiments the so called Maxwell Boltzmann distribution can be derived (see fig.

). This indicates the portion of the gas constituents having a specific velocity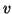

in thermal equilibrium (

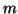denotes the mass of the particles). At www.gs68.de you can plot a Maxwell Boltzmann Distribution online.

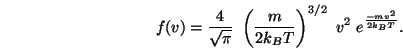$\begin{displaymath} f(v) = \frac{4}{\sqrt{\pi}} \left(\frac{m}{2 {\ensuremath... ...ight)^{3/2} v^2 e^{\frac{-m v^2}{2 {\ensuremath{k_B}}T}}. \end{displaymath}$

(1.7)

**Figure:** Maxwell Boltzmann distribution
$\resizebox{12cm}{!}{\includegraphics{maxwell_boltzmann}}$

The shape of the distribution gets wider for higher temperatures and also the peak decreases. It is possible to calculate a mean speed 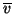$\overline{v}$ which is equal to:

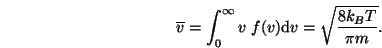$\begin{displaymath} \overline{v} = \int^\infty_0 v f(v) \mbox{d}v = \sqrt{\frac{8 {\ensuremath{k_B}}T}{\pi m}}. \end{displaymath}$

(1.8)

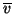The mean speed is always higher than the most probable speed due to the skewness of the distribution. For Argon atoms at $20^\circ$ C (=295K) $\overline{v}$ = 394m/s.

Next: Collision Parameters Up: Gases and Ideal Gases Previous: Kinetic Gas Theory Contents Index

back to www.gs68.de

Other important things: Legal Notice, Contact us